sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

        NÚMERO QUÂNTICO DO INFINITO-DIMENSIONAL  GRACELI.

ONDE TODA PARTE ÍNFIMA E INFINITÉSIMA DE ENERGIA POSSA SER REPRESNTADA DENTRO DE QUALQUER TIPO DE ÁTOMO, OU ESTRUTURA EM QUE SE ENCONTRE DENTRO DO SISTEMA INFINITO-DIMENSIONAL GRACELI.

OU SEJA, ONDE ENVOLVE TENSORES DE GRACELI, SDCTIE GRACELI, E O INFINITO-DIMENSIONAL .

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Uma teoria da variável escondida local na interpretação da mecânica quântica é uma teoria das variáveis ocultas que tem a necessidade adicional de ser consistente com o realismo local.^[1][2] Refere-se a todos os tipos de teoria que tentam explicar as características probabilísticas da mecânica quântica pelo mecanismo das variáveis inacessíveis subjacentes, com o requisito adicional do realismo local de que os eventos distantes sejam independentes, descartando instantaneamente (ou seja, mais rápido que a luz) interações entre eventos separados.

• 4Bibliografia

Estados quânticos com um modelo de variável oculta local

Para os estados separáveis^[3] de duas partículas, há um modelo variável oculto simples para quaisquer medições em duas partes. Surpreendentemente, também existem estados emaranhados para os quais todas as medidas de von Neumann podem ser descritas por um modelo de variável oculto. Esses estados estão embaraçados, mas não violam qualquer desigualdade de Bell. Os chamados estados de Werner são uma família de estados de um único parâmetro que são invariantes sob qualquer transformação do tipo ${\displaystyle U\otimes U,}$ onde ${\displaystyle U}$ é uma matriz unitária. Para dois qubits, eles são singletos ruidosos dados como

(4) ${\displaystyle \varrho =p\vert \psi ^{-}\rangle \langle \psi ^{-}\vert +(1-p){\frac {\mathbb {I} }{4}},}$ 

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde o singleto é definido como ${\displaystyle \vert \psi ^{-}\rangle ={\frac {1}{\sqrt {2}}}\left(\vert 01\rangle -\vert 10\rangle \right).}$

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

R. F. Werner mostrou que tais estados permitem um modelo de variável oculto para ${\displaystyle p\leq 1/2,}$ enquanto eles estão embaraçados se ${\displaystyle p>1/3}$. O limite para modelos variáveis ocultos poderia ser melhorado até ${\displaystyle p=0,66}$.^[4] Modelos variáveis ocultos foram construídos para os estados Werner,^[5] mesmo que as medições POVM sejam permitidas, não somente as medições de von Neumann.^[6] Além dos sistemas bipartidos, também há resultados para o caso multipartido. Um modelo de variável oculta para todas as medidas de von Neumann nos partidos foi apresentado para um estado quântico de três qubits.^[7]

Teoria de campo de Liouville

Origem: Wikipédia, a enciclopédia livre.

Na física, teoria de campo de Liouville, ou simplesmente (teoria de Liouville) é uma teoria quântica de campos bidimensional cuja equação clássica de movimento se assemelha a equação diferencial não-linear de segunda ordem de Joseph Liouville a que aparece no problema geométrico clássico de uniformização de superfícies de Riemann.

A teoria de campo é definida pela ação local:

${\displaystyle S={\frac {1}{4\pi }}\int d^{2}x{\sqrt {g}}(g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi +(b+b^{-1})R\phi +4\pi e^{2b\phi }),}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle \partial _{\mu }=\partial /\partial x^{\mu },\ g_{\mu \nu }}$ 

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

é a métrica do espaço bidimensional em que a teoria de campo é formulada, ${\displaystyle R}$ é o escalar Ricci de tal espaço, e ${\displaystyle b}$ é um acoplamento constante real. O campo ${\displaystyle \phi }$ é consequentemente chamado de campo Liouville.

A equação de movimento associado a esta ação é ::${\displaystyle \Delta \phi (x)={\frac {1}{2}}(b+b^{-1})R(x)+4\pi be^{2b\phi (x)}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle \Delta =g^{-1/2}\partial _{\mu }(g^{1/2}g^{\mu \nu }\partial _{\nu })}$ 

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

é o operador de d'Alembert nesse espaço. No caso, a métrica do espaço sendo a métrica Euclidiana e utilizando a notação padrão, torna-se a equação clássica de Liouville.

${\displaystyle \left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}\right)\phi (x,y)=4\pi be^{2b\phi (x,y)}}$^[1]

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A teoria de Chern-Simons, nomeada em homenagem a Shiing-Shen Chern e James Harris Simons, é uma teoria de campo quântico topológico tridimensional do tipo Schwarz, desenvolvida por Edward Witten.^[1] É assim chamado porque sua ação é proporcional à integral da forma 3 de Chern-Simons.^[2][3]

• 2Referências

A teoria clássica

Origem matemática

Na década de 1940, S. S. Chern e A. Weil estudaram as propriedades globais de curvatura de variedades lisas M como co-homologia de Rham (teoria de Chern-Weil), que é um passo importante na teoria de classes características em geometria diferencial.

Dado um fibrado G-principal plano P em M, existe um homomorfismo único, chamado homomorfismo de Chern-Weil, da álgebra de polinômios invariantes aditivos G em g (álgebra de Lie de G) à co-homologia ${\displaystyle H^{*}(M,\mathbb {R} )}$.^[4] Se o polinômio invariante for homogêneo, pode-se escrever concretamente qualquer forma k da conexão fechada ω como forma 2k da forma de curvatura associada Ω de ω.

Em 1974, S. S. Chern e J. H. Simons construíram concretamente uma forma (2k-1) df(ω) tal que

${\displaystyle dTf(\omega )=f(\Omega ^{k}),}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde T é o homomorfismo Chern-Weil. Esta forma é chamada de forma de Chern-Simons. Se df(ω) estiver fechado, pode-se integrar a fórmula acima

${\displaystyle Tf(\omega )=\int _{C}f(\Omega ^{k}),}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde C é um ciclo bidimensional (2k-1) em M. Esse invariante é chamado invariante de Chern-Simons. O invariante de Chern-Simons (M) é o termo de fronteira que não pode ser determinado por nenhuma formulação combinatória pura. Também pode ser definido como

${\displaystyle CS(M)=\int _{s(M)}{\tfrac {1}{2}}Tp_{1}\in \mathbb {R} /\mathbb {Z} ,}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle p_{1}}$ é o primeiro número de Pontryagin e s(M) é a seção do feixe ortogonal normal P.　Além disso, o termo Chern-Simons é descrito como o eta invariante definido por Atiyah, Patodi e Singer.

A invariância do medidor e a invariância métrica podem ser vistas como a invariância sob a ação do grupo de Lie adjacente na teoria de Chern-Weil. A integral de ação (integral do caminho) da teoria de campo na física é vista como a integral lagrangiana da forma de Chern-Simons e do loop de Wilson, holonomia do conjunto vetorial M. Isso explica por que a teoria de Chern-Simons está intimamente relacionada à teoria de campos topológicos.

Configurações

As teorias de Chern-Simons podem ser definidas em qualquer 3-variedade M topológica, com ou sem limite.^[5] Como essas teorias são teorias topológicas do tipo Schwarz, nenhuma métrica precisa ser introduzida em M.

A teoria de Chern-Simons é uma teoria de calibre, o que significa que uma configuração clássica na teoria de Chern-Simons em M com o grupo de calibre G é descrita por um pacote G principal on M. A conexão deste fibrado é caracterizado por uma conexão de forma única A, valorizada na álgebra de Lie g do grupo de Lie G.Em geral, a conexão A é definida apenas em fragmentos de coordenadas individuais, e os valores de A em fragmentos diferentes são relacionados por mapas conhecidos como transformações de gauge. Estes são caracterizados pela afirmação de que a derivada covariante, que é a soma do operador de derivada externa d e a conexão A, se transforma na representação adjunta do grupo de calibre G. O quadrado da derivada covariante consigo mesmo pode ser interpretado como uma forma bidimensional F com valor g chamada forma de curvatura ou força de campo. Também se transforma na representação adjunta.

Dinâmica

A ação S da teoria de Chern-Simons é proporcional à integral da forma tridimensional de Chern-Simons^[6]

${\displaystyle S={\frac {k}{4\pi }}\int _{M}{\text{tr}}\,(A\wedge dA+{\tfrac {2}{3}}A\wedge A\wedge A).}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A constante k é chamada de nível da teoria. A física clássica da teoria de Chern-Simons é independente da escolha do nível k.

Classicamente, o sistema é caracterizado por suas equações de movimento, que são os extremos da ação em relação às variações do campo A. Em termos da curvatura do campo

${\displaystyle F=dA+A\wedge A\,}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

a equação de campo é explicitamente

${\displaystyle 0={\frac {\delta S}{\delta A}}={\frac {k}{2\pi }}F.}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

As equações clássicas de movimento são, portanto, satisfeitas se, e somente se, a curvatura desaparecer em todos os lugares; nesse caso, a conexão é considerada plana. Assim, as soluções clássicas da teoria de G Chern-Simons são as conexões planas dos principais fibrados G on M. As conexões planas são determinadas inteiramente por holonomias em torno de ciclos incontratáveis na base M. Mais precisamente, elas estão em correspondência individual com classes de equivalência de homomorfismos do grupo fundamental de M ao grupo de medida G até a conjugação.

Se M tem um limite N, existem dados adicionais que descrevem uma escolha de trivialização do pacote G principal em N. Essa escolha caracteriza um mapa de N a G. A dinâmica desse mapa é descrita por modelo de Wess-Zumino-Witten (WZW) em N no nível k.

A Teoria do Funcional da Densidade (do inglês, Density Functional Theory, DFT) é uma das mais populares teorias da mecânica quântica utilizada para descrever propriedades eletrônicas na física do estado sólido, química quântica, ciência dos materiais, bioquímica, biologia, nano-sistemas e sistemas em escala atômica. Com essa teoria, as propriedades de um sistema com muitos elétrons podem ser determinadas aplicando funcionais, funções que recebem como argumento uma outra função, sobre a densidade eletrônica, o que origina o nome Teoria do Funcional da Densidade. A DFT é um dos métodos mais versáteis disponíveis em física da matéria condensada, física computacional e química computacional devido a generalidade de seus fundamentos e a flexibilidade de implementação. Os cálculos de DFT são ab initio (de primeiros princípios) não usam parâmetros experimentais ou empíricos e têm grande impacto na ciência dos materiais por seu poder preditivo com um custo computacional praticável.

• 7Referências

Visão geral

O tratamento quântico completo de um sistema de muitos elétrons, sob um potencial externo, deve considerar a repulsão coulombiana entre cada par de elétrons e a interação de spin. Esse problema não tem solução analítica, já que a função de onda total deve depender da distância entre todos os elétrons.

O método de Hartree-Fock (1930) é uma das teorias que busca resolver esse problema utilizando a função de onda como variável fundamental e apesar de apresentar resultados precisos, envolve um alto custo computacional^[1]. Já o modelo de Thomas-Fermi (1927), desenvolvido independentemente por Llewellyn Thomas e Enrico Fermi, é considerado o precursor da DFT e também busca resolver o problema quântico de muitos corpos. Essa é a primeira teoria a propor a determinação da estrutura eletrônica em termos da densidade, invés das funções de onda individuais de cada elétron. Esse modelo só é válido no limite de uma carga nuclear infinita e usá-lo para sistemas reais produz previsões quantitativas pobres.

Com a ideia inicial de Thomas-Fermi sobre o papel essencial da densidade eletrônica, Pierre Hohenberg e Walter Kohn (1964) demonstraram que a densidade eletrônica ${\displaystyle n(x,y,z)}$ determina completamente o problema quântico e pode ser usada para resolvê-lo de forma exata. Walter Kohn recebeu o prêmio Nobel de Química em 1998 por seu desenvolvimento da Teoria do Funcional da Densidade^[2].

Após seu desenvolvimento, a DFT tem sido utilizada para cálculos em física do estado sólido e, em muitos casos, os resultados concordam satisfatoriamente com os dados experimentais e os custos computacionais são relativamente baixos quando comparados ao método de Hartree-Fock. Entretanto, a DFT não era considerada precisa o suficiente para cálculos em química quântica até a década de 1990, quando os funcionais de troca e correlação foram refinados para prover um balanço entre custo computacional e precisão dos resultados.

Apesar das melhores aproximações para os funcionais de troca e correlação, ainda existem dificuldades em usar a DFT para descrever adequadamente as interações intermoleculares, especialmente as forças de van der Waals, as excitações de transferência de cargas, estados de transição, sistemas fortemente correlacionados e em cálculos do gap de energia em semicondutores.

Formalismo

Equação de Schrödinger

A Teoria do Funcional da Densidade busca resolver a equação de Schrödinger que descreve como o estado quântico de um sistema de muitos corpos evolui com o tempo^[3]. A equação abaixo é a equação de Schrödinger dependente do tempo em 3 dimensões ( ${\displaystyle \mathbf {r} }$ é o vetor posição que, em coordenadas cartesianas, pode ser escrito como ${\displaystyle \mathbf {r} =x{\hat {x}}+y{\hat {y}}+z{\hat {z}}}$)

${\displaystyle i\hbar {\frac {\partial \Psi (\mathbf {r} ,t)}{\partial t}}=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,t)}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ao utilizar o método de separação de variáveis, obtém-se a equação de Schrödinger independente do tempo

${\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right]\psi (\mathbf {r} )=E\psi (\mathbf {r} )}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

com o termo entre colchetes sendo o hamiltoniano, ${\displaystyle E}$ os valores de energia e ${\displaystyle \psi (\mathbf {r} )}$ os autoestados do sistema independentes do tempo. Essa equação pode ser escrita como uma equação de autovalores e autovetores da forma

${\displaystyle H\psi (\mathbf {r} )=E\psi (\mathbf {r} )}$.///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Aproximação de Born-Oppenheimer

Para a descrição quântica completa de um sistema atômico ou molecular, o hamiltoniano deve incluir tanto o movimento dos núcleos como o dos elétrons, bem como a interação entre todos os corpos. Assim, o hamiltoniano completo é dado por

${\displaystyle H={\hat {T_{N}}}+{\hat {T_{e}}}+{\hat {V_{Ne}}}+{\hat {V_{e}}}+{\hat {V_{N}}}}$

onde ${\displaystyle {\hat {T_{N}}}}$ é a energia cinética dos núcleos, ${\displaystyle {\hat {T_{e}}}}$ a energia cinética dos elétrons, ${\displaystyle {\hat {V_{Ne}}}}$ a energia de atração elétron-núcleo, ${\displaystyle {\hat {V_{e}}}}$ a interação repulsiva entre os elétrons e ${\displaystyle {\hat {V_{N}}}}$ é a energia potencial de repulsão núcleo-núcleo^[1].

Ao considerar esse hamiltoniano, a equação de Schrödinger para um sistema de muitos corpos não possui solução analítica e aproximações são necessárias. A primeira aproximação é a de Born-Oppenheimer que desacopla o movimento dos elétrons ao dos núcleos. Essa aproximação é razoável, já que a massa dos núcleos é muito maior que a dos elétrons que se rearranjam rapidamente após qualquer alteração na posição dos núcleos^[4]. Com isso, a energia cinética dos núcleos se torna um termo constante em relação ao movimento dos elétrons, e o hamiltoniano pode ser escrito como

${\displaystyle {H}={H}_{ele}+{\hat {V}}_{N}}$

onde

${\displaystyle {H}_{ele}={\hat {T}}_{e}+{\hat {V}}_{Ne}+{\hat {V}}_{e}}$

é denominado hamiltoniano eletrônico. A equação de Schrödinger para todos os elétrons do sistema é

${\displaystyle {H}_{ele}\psi _{e}=E\psi _{e}}$

onde ${\displaystyle \psi _{e}}$ é a função de onda total do sistema eletrônico e ${\displaystyle E}$ é a energia.

Teoremas de Hohenberg e Kohn

A Teoria do Funcional da Densidade está embasada em dois teoremas propostos por P. Hohenberg e W. Kohn (HK)^[5] em 1964. Os teoremas são válidos para um sistema constituído por um número arbitrário de elétrons confinados numa caixa, sujeitos a um potencial externo ${\displaystyle v(\mathbf {r} )}$ e à repulsão coulombiana mútua.

1º Teorema: O potencial externo ${\displaystyle v(\mathbf {r} )}$ sentido pelos elétrons é um funcional único da densidade eletrônica ${\displaystyle n(\mathbf {r} )}$.

A prova deste teorema é feita por reductio ad absurdum. Considerando o hamiltoniano eletrônico ${\displaystyle H_{ele}}$

${\displaystyle H_{ele}=T+U+V}$

onde a energia cinética total ${\displaystyle T}$, a energia potencial proveniente do potencial externo ${\displaystyle V}$ e a repulsão coulombiana ${\displaystyle U}$ são dados por

${\displaystyle T={\frac {1}{2}}\int {\nabla \psi ^{*}(\mathbf {r} )\nabla \psi (\mathbf {r} )d\mathbf {r} }}$

${\displaystyle V=\int {v(\mathbf {r} )\psi ^{*}(\mathbf {r} )\psi (\mathbf {r} )d\mathbf {r} }}$

${\displaystyle U={\frac {1}{2}}\int {{\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\psi ^{*}(\mathbf {r} )\psi (\mathbf {r} ')\psi (\mathbf {r} ')\psi (\mathbf {r} )d\mathbf {r} d\mathbf {r} '}}$

Por simplicidade, supõe-se que o estado fundamental é não degenerado e a densidade eletrônica nesse estado é dada por

${\displaystyle n(\mathbf {r} )=\int {\Psi ^{*}(\mathbf {r} )\Psi (\mathbf {r} )d\mathbf {r} }}$

Agora, suponha que outro potencial ${\displaystyle v'(\mathbf {r} )}$, associado ao hamiltoniano ${\displaystyle H'_{ele}}$

${\displaystyle H'_{ele}=T+V'+U}$

com estado fundamental ${\displaystyle \Psi '}$ e energia ${\displaystyle E'}$, dê origem a mesma densidade ${\displaystyle n(\mathbf {r} )}$.

Para ${\displaystyle \Psi }$ ser diferente de ${\displaystyle \Psi '}$, ${\displaystyle v'(\mathbf {r} )-v(\mathbf {r} )}$ necessariamente não é uma constante e as funções de onda satisfazem diferentes equações de Schrödinger. Pelo princípio variacional, a energia do estado fundamental é mínima para função de onda exata daquele estado, de forma que as desigualdades abaixo são válidas.

${\displaystyle E'=\langle \Psi '|H'_{ele}|\Psi '\rangle <\langle \Psi |H'_{ele}|\Psi \rangle =\langle \Psi |H_{ele}+V'-V|\Psi \rangle }$

${\displaystyle E'<E+\int {[v'(\mathbf {r} )-v(\mathbf {r} )]n(\mathbf {r} )d\mathbf {r} }}$

${\displaystyle E<E'+\int {[v(\mathbf {r} )-v'(\mathbf {r} )]n(\mathbf {r} )d\mathbf {r} }}$

Ao somar as duas desigualdades obtém-se:

${\displaystyle E'+E<E+E'}$

que é uma inconsistência. Dessa forma, assumir que a densidade é igual para ${\displaystyle v'(\mathbf {r} )\neq v(\mathbf {r} )}$ gera um absurdo decorrente de ${\displaystyle \Psi }$ ser necessariamente diferente de ${\displaystyle \Psi '}$. Conclui-se que a unicidade de ${\displaystyle n(\mathbf {r} )}$ exige que ${\displaystyle \Psi =\Psi '}$ e ${\displaystyle v'(\mathbf {r} )-v(\mathbf {r} )}$ seja constante, portanto, o potencial externo é um funcional único da densidade eletrônica.

O 1º teorema de HK demonstra que a densidade pode ser a variável fundamental na determinação da estrutura eletrônica e isso é sumarizado pela sequência abaixo

${\displaystyle n(\mathbf {r} )\Rightarrow \Psi \Rightarrow v(\mathbf {r} )\Rightarrow {\text{Observáveis}}}$

onde o conhecimento da densidade eletrônica implica no conhecimento da função de onda e do potencial externo que determina o hamiltoniano do sistema e, consequentemente, todos os observáveis no estado fundamental.

2º Teorema: A energia do estado fundamental é mínima para densidade ${\displaystyle n(\mathbf {r} )}$ exata.

O segundo teorema expressa que a energia do estado fundamental é um funcional da densidade eletrônica cujo valor mínimo é obtido para densidade exata. Para provar esse teorema, considere o funcional

${\displaystyle E_{v}[n(\mathbf {r} )]\equiv \int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+F[n(\mathbf {r} )]}$

onde

${\displaystyle F[n(\mathbf {r} )]=\langle \Psi |T+U|\Psi \rangle }$

é denominado funcional universal. Do método variacional, o funcional ${\displaystyle \epsilon _{v}}$ da função de onda ${\displaystyle \Psi '}$

${\displaystyle \epsilon _{v}[\Psi ']=\langle \Psi '|V|\Psi '\rangle +\langle \Psi '|T+U|\Psi '\rangle }$

é mínimo para o estado fundamental ${\displaystyle \Psi }$. Se ${\displaystyle \Psi '}$ for o estado fundamental associado ao potencial externo ${\displaystyle v'(\mathbf {r} )}$, a seguinte relação é válida

${\displaystyle \epsilon _{v}[\Psi ']=\int {v(\mathbf {r} )n'(\mathbf {r} )d\mathbf {r} }+F[n'(\mathbf {r} )]>\epsilon [\Psi ]=\int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+F[n(\mathbf {r} )]}$

de forma que

${\displaystyle \epsilon [n'(\mathbf {r} )]>\epsilon [n(\mathbf {r} )]}$

como se queria demonstrar. Em linhas gerais, o segundo teorema de HK apresenta um critério para determinar a densidade do estado fundamental.

Se ${\displaystyle F[n(\mathbf {r} )]}$ for um funcional conhecido, o problema de determinar a densidade e energia do estado fundamental de um sistema eletrônico em dado potencial externo se reduz a minimização do funcional ${\displaystyle E_{v}[n]}$. Como as interações de Coulomb são de longo alcance, é conveniente separar essa interação do funcional universal

${\displaystyle F[n]={\frac {1}{2}}\int {{\frac {n(\mathbf {r} )n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} d\mathbf {r} '}+G[n]}$

e definir o funcional ${\displaystyle G[n]}$ que deve estar relacionado às energias cinética, de troca e correlação dos elétrons. Apesar da aproximação de Born-Oppenheimer, o desenvolvimento da teoria é exato até esse ponto, entretanto, não é conhecida nenhuma forma analítica para o funcional ${\displaystyle G[n]}$ e aproximações devem ser tomadas para que seja possível determinar a densidade eletrônica do estado fundamental.

Equações de Kohn-Sham

W. Kohn e L. J. Sham (1965)^[6] foram os primeiros a apresentar uma tática para determinar a estrutura eletrônica de sistemas com muitos elétrons a partir da minimização do funcional ${\displaystyle E_{v}}$.

O ansatz de Kohn-Sham propõe que a densidade do estado fundamental de um sistema com elétrons interagentes seja igual à densidade do estado fundamental de um sistema fictício com elétrons não interagentes em um potencial efetivo, de forma que o funcional universal ${\displaystyle G[n]}$ é dado por

${\displaystyle G[n]\equiv T_{s}[n]+E_{xc}[n]}$

onde ${\displaystyle T_{s}[n]}$ é a energia cinética do sistema não interagente com densidade ${\displaystyle n(\mathbf {r} )}$ e ${\displaystyle E_{xc}[n]}$ é a energia de troca e correlação de um sistema interagente de mesma densidade ${\displaystyle n(\mathbf {r} )}$. Com isso, o funcional de energia que deve ser minimizado é

${\displaystyle E_{v}[n]=\int {v(\mathbf {r} )n(\mathbf {r} )d\mathbf {r} }+{\frac {1}{2}}\int {{\frac {n(\mathbf {r} )n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} d\mathbf {r} '}+T_{s}[n]+\int {n(\mathbf {r} )E_{xc}[n(\mathbf {r} )]d\mathbf {r} }}$

A resolução do problema de muitos corpos esbarra num funcional com fórmula analítica não conhecida ${\displaystyle E_{xc}[n]}$ e, posteriormente, será necessário aproximar esse termo.

A densidade eletrônica exata é um extremo do funcional de energia ${\displaystyle E_{v}}$ e a carga eletrônica total do sistema de ${\displaystyle N}$ elétrons é fixa, de forma que a equação abaixo é um vínculo

${\displaystyle \int {n(\mathbf {r} )d\mathbf {r} }=N}$

De acordo com o método variacional, incluindo esse vínculo, deve-se ter

${\displaystyle \int {\delta n(\mathbf {r} ){\bigg (}{\frac {\delta T_{s}}{\delta n}}+v(\mathbf {r} )+\int {{\frac {n(\mathbf {r'} )}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} '}+v_{xc}[n]-\mu {\bigg )}d\mathbf {r} }=0}$

onde ${\displaystyle \mu }$ é o multiplicador de Lagrange e ${\displaystyle v_{xc}[n]={\frac {\delta E_{xc}}{\delta n}}}$ é o potencial de troca e correlação.

A energia cinética do sistema fictício não interagente, em unidades atômicas, é

${\displaystyle T_{s}[n]=-{\frac {1}{2}}\sum _{i}\int {\psi _{i}^{*}\nabla ^{2}\psi _{i}d^{3}r}}$

e do ansatz de KS decorre que

${\displaystyle n(\mathbf {r} )=\sum _{i=1}^{N}|\psi _{i}(\mathbf {r} )|^{2}}$

é a densidade do estado fundamental.

A solução da equação de minimização que deve resultar em ${\displaystyle n(\mathbf {r} )}$ pode ser obtida da equação de Schrödinger de uma partícula, já que no sistema fictício os elétrons não interagem

${\displaystyle {\hat {h}}^{KS}\psi _{i}(\mathbf {r} )={\bigg (}-{\frac {1}{2}}\nabla ^{2}+v^{KS}[n]{\bigg )}\psi _{i}(\mathbf {r} )=\epsilon _{i}\psi _{i}(\mathbf {r} )}$.

Essa equação é denominada equação de Kohn-Sham, ${\displaystyle {\hat {h}}^{KS}}$ é o hamiltoniano de KS e

${\displaystyle v^{KS}=v(\mathbf {r} )+\int {{\frac {n(\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d\mathbf {r} '}+v_{xc}[n]}$

é o potencial efetivo de Kohn-Sham. Normalmente, ${\displaystyle \psi _{i}}$ são ditos orbitais de KS e é importante destacar que esses orbitais não são as funções de onda do sistema interagente, tal como ${\displaystyle \epsilon _{i}}$ não é autovalor de energia do sistema real; apenas a densidade do estado fundamental ${\displaystyle n(\mathbf {r} )}$ é igual nos sistemas real e fictício.

É necessário resolver a equação de KS para determinar a densidade eletrônica, entretanto, ${\displaystyle v^{KS}}$ depende de ${\displaystyle n(\mathbf {r} )}$ e não é possível resolver a equação diretamente. Nesse caso, comumente, é adotado um cálculo autoconsistente.

Método de cálculo autoconsistente

Cálculo autoconsistente em DFT

A equação de KS pode ser resolvida através de um cálculo autoconsistente: a partir de uma densidade inicial ${\displaystyle n^{j}}$, calcula-se o potencial efetivo de Kohn-Sham ${\displaystyle v^{KS}(\mathbf {r} )}$ e determinam-se as funções de onda ${\displaystyle \psi _{i}(\mathbf {r} )}$ pela solução da equação de KS. Em seguida, calcula-se a densidade do estado fundamental ${\displaystyle n^{j+1}}$ a partir desses orbitais e compara-se com a densidade inicial: se ${\displaystyle n^{j+1}=n^{j}}$ , diz-se que o cálculo convergiu e a densidade ${\displaystyle n^{j+1}}$ pode ser utilizada para determinar os observáveis físicos; caso contrário, ${\displaystyle n^{j+1}}$ é utilizado para calcular o potencial efetivo, o ciclo de autoconsistência é reiniciado e esse processo continua até o cálculo convergir.

A densidade eletrônica inicial é arbitrária e, normalmente, é uma distribuição aleatória. Note que para calcular o potencial efetivo de KS é preciso, a priori, aproximar o funcional de troca e correlação ${\displaystyle E_{xc}}$, portanto, para iniciar o cálculo autoconsistente devem ser feitas, inicialmente, duas escolhas: densidade eletrônica inicial e a forma de ${\displaystyle E_{xc}}$.

Funcionais de Troca e Correlação

A escolha do funcional de troca e correlação é um fator decisivo para o precisão da DFT e um dos aspectos mais atraentes dessa teoria é que mesmo as aproximações mais simples para esse funcional podem fornecer resultados precisos. As aproximações para ${\displaystyle E_{xc}}$ podem ser separadas em: funcionais locais (como TF, LDA e LSDA onde esse último inclui a polarização de spin), funcionais dependentes do gradiente (GEA e GGA) e funcionais não locais (híbridos DFT, meta-GGA e EXX, etc).

LDA

Na aproximação LDA (do inglês, Local Density Approximation), supõe-se que a energia de troca e correlação de um sistema inomogêneo de densidade ${\displaystyle n(\mathbf {r} )}$ no ponto ${\displaystyle r}$ é igual à energia de troca e correlação de um gás de elétrons homogêneo com a mesma densidade. O funcional ${\displaystyle E_{xc}}$, para um sistema sem polarização de spin, é escrito como

${\displaystyle E_{xc}^{LDA}[n]=\int {n(\mathbf {r} )\epsilon _{xc}(n(\mathbf {r} ))d\mathbf {r} }}$

onde ${\displaystyle \epsilon _{xc}(n)}$ é a energia de troca e correlação por elétron do gás de densidade constante ${\displaystyle n(\mathbf {r} )}$. Com isso, o potencial de troca e correlação

${\displaystyle v_{xc}[n]={\frac {\delta E_{xc}}{\delta n}}={\frac {d}{dn(\mathbf {r} )}}{\big [}n(\mathbf {r} )\epsilon _{xc}(n(\mathbf {r} )){\big ]}}$

depende apenas da densidade no ponto ${\displaystyle \mathbf {r} }$.

A energia de troca e correlação por elétron é decomposta linearmente nessas interações, de forma que

${\displaystyle E_{xc}\approx E_{xc}^{LDA}[n]=\int {n(\mathbf {r} )[\epsilon _{x}(n(\mathbf {r} ))+\epsilon _{c}(n(\mathbf {r} ))]d\mathbf {r} }}$

onde energia de troca ${\displaystyle \epsilon _{x}}$ do gás homogêneo é conhecida analiticamente^[7] e a energia de correlação ${\displaystyle \epsilon _{c}}$ deve ser parametrizada ou determinada através de outras simulações computacionais.

D. M. Ceperley e B. J. Alder (1980) determinaram ${\displaystyle \epsilon _{c}}$ com grande precisão para certos valores de densidade a partir de uma simulação com Monte Carlo Quântico para o gás homogêneo e interagente^[8]. A partir desses valores, J. Perdew e A. Zunger (1981) propuseram uma parametrização para ${\displaystyle \epsilon _{xc}}$ conhecido como LDA-PZ^[9]. Por muitos anos, a aproximação LDA foi utilizada no cálculo de estruturas de banda e energia total já que apresenta bons resultados mesmo para sistemas com densidade não uniforme e isso se deve a um cancelamento sistemático: a energia de correlação é subestimada, enquanto a de troca é superestimada^[10].

GGA

Se a densidade eletrônica for não uniforme, a aproximação LDA não descreve bem os sistemas reais que são inomogêneos, já que os elétrons estão sujeitos a variação espacial do campo elétrico dos núcleos e se repelem mutuamente. Nesse contexto, surge a aproximação GGA (do inglês, Generalized Gradient Approximation) que considera a variação espacial da densidade ${\displaystyle n(\mathbf {r} )}$ ao propor que o funcional de troca e correlação seja expresso em termos de ${\displaystyle n(\mathbf {r} )}$ e ${\displaystyle \nabla n(\mathbf {r} )}$. Genericamente:

${\displaystyle E_{xc}\approx E_{xc}^{GGA}[n]=\int {f{\big (}n(\mathbf {r} ),\nabla n(\mathbf {r} ){\big )}d\mathbf {r} }}$.

Existem várias escolhas para a função ${\displaystyle f}$ e isso implica em diferentes aproximações GGA, como os funcionais PBE (proposto por J. P. Perdew, Kieron Burke e Matthias Ernzerhof em 1996^[11]) e BLYP (que combina o funcional de troca proposto por A. D. Becke (1988)^[12] com o funcional de correlação formulado no mesmo ano por C. Lee, W. Yang e R. Parr^[13]). As aproximações GGA descrevem bem as ligações químicas, mas falham na descrição de interações fracas como as forças de van der Waals.

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A Teoria quântica dos campos locais, ou Sistema axiomático Haag-Kastler para a teoria quântica dos campos, ou ainda Teoria quântica dos campos algébrica foi proposta pelos físicos Rudolf Haag e Daniel Kastler em 1964.

A teoria é uma aplicação local da física quântica numa C*-álgebra. Os axiomas desta teoria são definidos em termos algébricos dados por todo conjunto aberto num espaço de Minkowski, e mapeados entre eles.

Definição

Permitindo que Mink seja a categoria de subconjuntos abertos de um espaço de Minkowski M com função inclusão como morfismo. É dado um functor contravariante ${\displaystyle {\mathcal {A}}}$ de Mink para uC*alg, a categoria de C*álgebras unitais, já que todo morfismo em Mink se mapeia para um monomorfismo num uC*alg.

O grupo de Poincaré age continuamente no Mink. Ali existe o produto fibrado desta ação, que é continua na norma operacional da Covariância de Lorentz: ${\displaystyle {\mathcal {A}}(M)}$.///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O espaço de Minkowski possui uma estrutura casual. Logo se um conjunto aberto V se encontra no complemento casual de um conjunto aberto U, então a imagem do mapeamento

${\displaystyle {\mathcal {A}}(i_{U,U\cup V})}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e

${\displaystyle {\mathcal {A}}(i_{V,U\cup V})}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Comuta se ${\displaystyle {\bar {U}}}$ é o complemento casual do conjunto aberto U, então ${\displaystyle {\mathcal {A}}(i_{U,{\bar {U}}})}$ é um isomorfismo.

Um estado com respeito a uma C*-álgebra é uma Função linear positiva com norma unitária. Se nós possuirmos um estado sobre ${\displaystyle {\mathcal {A}}(M)}$, nós podemos obter o traço parcial e conseguir estados associados com ${\displaystyle {\mathcal {A}}(U)}$ para cada

Leitura recomendada///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 conjunto aberto.

Em física, teoria de gauge na rede é o estudo de teorias de gauge em um espaço-tempo discreto numa rede.^[1] Embora a maioria das teorias de gauge não sejam exatamente solúveis, são de grande utilidade pois podem ser estudadas por simulações computacionais. Espera-se que, executando simulações em rede progressivamente maiores, o comportamento da teoria correspondente no contínuo seja recuperado.

Nas teorias de gauge na rede o espaço-tempo passa por uma rotação de Wick, resultando em um espaço euclidiano, descrito por uma rede hiperretangular com espaçamento igual a ${\displaystyle a}$ entre seus sítios. Os campos de quarks são somente definidos nos sítios da rede. Há problemas com a duplicação de férmion, apesar de tudo. Ver ação de Wilson-Ginsparg. Em vez de um vetor potencial, como no caso contínuo, os campos de gauge são definidas sobre as ligações do retículo e correpondem ao transporte paralelo ao longo da borda que assume valores no grupo de Lie em questão. Daí para simular a cromodinâmica quântica (QCD), para que o grupo de Lie é SU(3), existe uma matriz especial unitária 3 por 3 definida em cada ligação. As faces do retículo são chamadas plaquetas. A ação de Yang-Mills é reescrita usando laços de Wilson sobre plaquetas (isto é simplesmente um "caráter" valorado sobre a composição de variáveis de ligação em torno da plaqueta) de tal forma que o limite ${\displaystyle a\to 0}$ formalmente dá a ação de contínuo original.

Mais precisamente, nós temos um retículo com vértices, grafos e faces. Em teoria de retículo, a terminologia alternativa sítios, ligações e plaquetas para vértices, grafos e faces é frequentemente usada. Isto reflete a origem do campo em física do estado sólido. Enquanto que cada grafo não tem orientação intrínseca, para definir as variáveis gauge, nós atribuimos um elemento de um grupo de Lie compacto G a cada grafo uma orientação para ele chamada U. Basicamente, a atribuição para um grafo em uma dada orientação é o grupo inverso da atribuição do mesmo grafo na orientação oposta. Igualmente, as plaquetas não têm orientação intrínseca, mas lhe são dadas temporariamente uma orientação para propósitos computacionais. Dada uma representação irredutível fiel ρ de G, o retículo ação de Yang-Mills é

${\displaystyle S=\sum _{F}-\Re \{\chi ^{(\rho )}(U(e_{1})\cdots U(e_{n}))\}}$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(a soma sobre todos os sítios do retículo do (componente real do) laço de Wilson). Aqui, χ é o "caráter" (traço) e o componente real é redundante se ρ passa a ser uma representação real ou pseudoreal. e₁, ..., e_n são os n grafos do laço de Wilson em sequência. O lado positivo sobre ser real é que se a orientação de um laço de Wilson é trocada, sua contribuição para a ação permanece inalterada.

Há muitas ações de Yang-Mills possíveis sobre o retículo, dependendo sobre qual laço de Wilson for usado a fórmula acima. A mais simples é a ação de Wilson, na qual o laço de Wilson é apenas uma plaqueta. Uma desvantagem da ação de Wilson é que a diferença entre ela e a ação contínua é proporcional ao espaçamento do retículo ${\displaystyle a}$. É possível usar laços de Wilson mais complexos onde esta diferença é proporcional a ${\displaystyle a^{2}}$, tornando as computações mais precisas. Estas são conhecidas como "ações melhoradas".

Para calcular uma grandeza (tal como a massa de uma partícula) em teoria de retículo gauge, ela deve ser calculada para cada valor possível do campo gauge sobre cada ligação, e então calculada sua média. Na prática isto é impossível. Em vez disso o método de Monte Carlo é usado para estimar a grandeza. Configurações aleatórias (valores de campos gauge) são geradas com probabilidades proporcionais a ${\displaystyle e^{-\beta S}}$, onde ${\displaystyle S}$ é a ação de retículo para que a configuração e ${\displaystyle \beta }$ seja relacionada ao espaçamento do retículo ${\displaystyle a}$. A grandeza é calculada para cada configuração. O verdadeiro valor da grandeza é então encontrado por tomar-se a média do valor de um grande número de configurações. Para encontrar o valor da grandeza na teoria contínua isto é repetido para vários valores de ${\displaystyle a}$ e extrapolados a ${\displaystyle a=0}$.

Teoria do retículo gauge é uma ferramenta importante para cromodinâmica quântica (QCD). A versão discreta da QCD é chamada retículo QCD. O confinamento QCD tem sido apresentado em simulações de Monte Carlo. Confinamento a alta temperatura conduz à formação de um plasma de quarks-glúons.

Teoria do retículo gauge tem-se mostrado exatamente duplas de espuma de spin desde que somente laços de Wilson apareçam na ação sobre plaquetas.

Lagrangiana

A dinâmica dos quarks e glúons é controlada pela lagrangiana da cromodinâmica quântica. A lagrangiana invariante de gauge da QCD é 

${\displaystyle {\mathcal {L}}_{\mathrm {QCD} }={\bar {\psi }}_{i}\left(i(\gamma ^{\mu }D_{\mu })_{ij}-m\,\delta _{ij}\right)\psi _{j}-{\frac {1}{4}}G_{\mu \nu }^{a}G_{a}^{\mu \nu }}$

onde ${\displaystyle \psi _{i}(x)\,}$ são os campos dos quarkos, uma função dinâmica do espaço tempo, na representação fundamental dogrupo de gauge SU(3), indexada por ${\displaystyle i,\,j,\,\ldots }$; ${\displaystyle {\mathcal {A}}_{\mu }^{a}(x)\,}$ são os campos de glúons, também funções dinâmicas do espaço-tempo, na representação adjunta do grupo de gauge SU(3), indexado por a, b,... ; γ^μ são as matrizes de Dirac conectando a representação spinorial a representação vetorial do grupo de Lorentz. 

O símbolo ${\displaystyle G_{\mu \nu }^{a}\,}$ representa o tensor de força do campo de glúon invariante de gauge, análogo ao tensor de força do campo eletromagnético, F^{\mu \nu} \,, em eletrodinâmica quântica. É dado por:^[8]

onde f_abc são as constantes de estrutura de SU(3). Note que as regras para mover os índices a, b, or c de cima para baixo são triviais (assinatura (+, ..., +)) de forma que f^abc = f_abc = f^a_bc ao passo que para os índices μ or ν devem ser seguidas as regras não triviais, correspondendo a assinatura métrica (+ − − −), por exemplo.

As constantes m e g controlam a massa dos quarks e as constantes de acoplamento da teoria, sujeitas a renormalização da teoria quântica completa.

Uma noção teórica importante envolvendo o termo final da lagrangiana acima é a variável do loop de Wilson. Esse loop tem papel importante nas formas discretizadas da QCD (veja QCD na rede), e de forma mais geral, distingue entre estados confinados e livres da teoria de gauge. Foi introduzido pelo físico laureado com Nobel Kenneth G. Wilson.

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Relação com física do estado sólido

Há relações inesperadas com a física do estado sólido. Por exemplo, a noção de invariaância de gauge forma a base para os vidros de Spin de Mattis,^[14] que são sistemas cujos graus de liberdade usuais ${\displaystyle s_{i}=\pm 1\,}$ com i =1,...,N, com os acoplamentos "aleatórios" especialmente adotados ${\displaystyle J_{i,k}=\epsilon _{i}\,J_{0}\,\epsilon _{k}\,.}$ Aqui ε_i e ε_k são quantidades independentes e que adotam aleatoriamente os valores ±1, o que corresponde a transformação de gauge mais simples${\displaystyle (\,s_{i}\to s_{i}\cdot \epsilon _{i}\quad \,J_{i,k}\to \epsilon _{i}J_{i,k}\epsilon _{k}\,\quad s_{k}\to s_{k}\cdot \epsilon _{k}\,)\,.}$ Isso significa que o valor termodinâmico esperado das quantidades mensuráveis, por exemplo a energia${\displaystyle {\mathcal {H}}:=-\sum s_{i}\,J_{i,k}\,s_{k}\,,}$ são invariantes.

Entretanto, aqui os graus de liberdade de acoplamento  ${\displaystyle J_{i,k}}$, que no caso da QCD correspondem aos glúons, estão "congelados" em valores fixos (quenching).Em contraste, na QCD eles "flutuam" (annealing), e através de um grande número de graus de liberdade a entropia tem papel importante.

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Principais energias em estrutura de bandas para sólidos cristalinos.

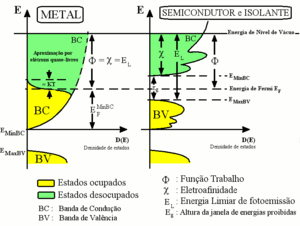
Há um limite máximo de energia cinética E_cin na qual elétrons fotoemitidos podem ser detectados em espectos oriundos de técnicas de espectroscopia eletrônica. Os elétrons mais energéticos emitidos pela amostra provêm, em acordo com a equação fundamental de fotoemissão, dos níveis com menores energias de ligação ocupados dentro da amostra, e mantêm relação direta com a densidade de estados associada a estes níveis. A energia de limiar de emissão (E_T ou E_L), muitas vezes chamada de energia de ionização do material (I), ^[1] refere-se ao módulo da energia dos elétrons mais energéticos detectáveis ^[2] em espectros de fotoemissão quando ainda não excitados e dentro do sólido, medida em referência ao nível de vácuo.

Outra forma de se definir energia de limiar de fotoemissão é dizer que esta corresponde à mínima energia ${\displaystyle \hbar \omega }$ que um fóton deve ter para conseguir arrancar elétrons da amostra, produzindo então uma corrente de fotoemissão.

Em semicondutores, onde o número de elétrons na banda de condução é mínimo à temperatura ambiente, não sendo estes detectáveis em espectros de fotoemissão, os elétrons mais energéticos detectáveis correspondem aos elétrons no topo da banda de valência. Em metais, os elétrons mais energéticos têm energias que excedem a energia de Fermi em um valor igual à energia térmica por eles ganha, geralmente aceita, em média, como sendo a metade do valor K_B T. Para T = 300K, K_BT = 0,025eV, muito aquém da resolução mínima do nosso espectrômetro de fotoelétrons.

Do exposto, define-se o limiar de fotoemissão E_T como sendo a soma da eletroafinidade X e a largura da janela de energias proibidas E_g (gap):

E_T = X + E_g

Como em semicondutores a eletroafinidade X localiza a energia E_MBC do mínimo da banda de condução em relação à energia de vácuo E_v (ver figura), e a energia E_g corresponde à distância em energia entre o mínimo da banda de condução e o máximo da banda de valência, o limiar de fotoemissão localiza a posição do topo da banda de valência em relação ao nível de vácuo. Em metais, não há faixa proibida acima dos níveis mais energéticos ocupados na banda de valência, pois esta banda encontra-se semipreenchida. Assim sendo, o limiar de fotoemissão corresponde à energia de Fermi do referido metal, dado que X = ${\displaystyle \Phi }$ nos metais.

Assim:

E_T = X + E_g = -E_v^MBV para semicondutores e isolantes, e

E_T = X = ${\displaystyle \Phi }$ para os metais.

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A equação de Born-Landé fornece o valor da energia reticular de um composto iônico. Em 1918^[1] Max Born e Alfred Landé propuseram que a energia da rede cristalina poderia ser derivada a partir do potencial eletrostático da rede iônica e do termo de energia potencial repulsiva.^[2]

${\displaystyle E=-{\frac {N_{A}Mz^{+}z^{-}e^{2}}{4\pi \epsilon _{o}r_{0}}}\left(1-{\frac {1}{n}}\right)}$ (Joules/mol)

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde

${\displaystyle \,N_{A}}$ = número de Avogadro

${\displaystyle \,M}$ = constante de Madelung, relacionada com a geometria do cristal.

${\displaystyle \,z^{+}}$ = carga do cátions em unidade eletrostática

${\displaystyle \,z^{-}}$ = carga do ânion em unidade eletrostática

${\displaystyle \,e}$ = carga elementar, 1,6022×10⁻¹⁹ C

${\displaystyle \,\epsilon _{o}}$ = permissividade, ${\displaystyle \,4\pi \epsilon _{o}}$ = 8,8541878176×10⁻¹² F m

${\displaystyle \,r_{0}}$ = distância do íon mais próximo em metros

${\displaystyle \,{n}}$ = expoente de Born, um número entre 5 e 12, determinado experimentalmente pela medida de compressibilidade do sólido ou derivado teoricamente.^[3]

A Natureza dos Espectros XPS

Espectro XPS para Arsenieto de gálio (100): os pícos salientes devem-se aos elétrons nas camadas eletrônicas indicadas. Todo o espectro se assenta sobre uma base que eleva-se para energias cinéticas menores e devida aos elétros secundários (espalhamento inelástico).

Na Espectroscopia de Fotoelétrons de Raios X, fótons de raios X, ao incidirem na amostra, interagem com os elétrons do material, transferindo-lhes energia. Dos elétrons participantes do processo, uma parcela ganhará energia suficiente e mover-se-á em direção adequada de forma que, ao atingirem a superfície da amostra, estes serão capazes de abandoná-la, ejetando-se para o ambiente externo, normalmente o interior de uma câmara de vácuo. Os elétrons ejetados da amostra podem ser coletados por um analisador de elétrons capaz de contar o número de elétrons que saem da amostra com determinada energia (velocidade) em um dado intervalo de tempo. Os espectros obtidos através deste processo são portanto curvas de Contagem x Energia como a mostrada ao lado. Na figura vêem-se também identificadas algumas estruturas – alguns picos de caroço - que refletem a estrutura de bandas inerente à amostra em análise.

Em função da estrutura de bandas ser individual e diferente para cada elemento químico, cada um dos elementos químicos terá um espectro XPS único e diferente dos demais, podendo os espectros serem facilmente utilizados para se identificar a presença ou não de um dado elemento na superfície da amostra, algo similar a uma impressão digital na mão de um datiloscopista. Uma relação de espectros para todos os elementos químicos conhecidos encontra-se há muito na literatura,^[2] e os espectros dos compostos químicos são, ressalvadas características próprias, em primeira aproximação a soma dos espectros individuais para os elementos que compõem a substância ou dos elementos que encontram-se por ventura juntos na superfície da amostra em análise.

Nos espectros há flutuações de naturezas diversas superpostas à resposta ideal. Há uma dispersão em certos casos considerável dos pontos experimentais em torno dos valores ideais esperados devido às interferências aleatórias inerentes à própria natureza do sistema, ou às que ocorrem durante o processo de medida. Um tratamento estatístico torna-se, portanto, indispensável, e para obter-se um espectro como o da figura, a faixa de energia considerada deve ser varrida várias vezes, obtendo-se, assim, vários valores experimentais associados a uma mesma energia. Uma média desses valores é automaticamente realizada pelo software de controle do equipamento de medida - que cuida também do controle das várias varreduras necessárias- e o valor médio é o valor assumido no espectro final - o valor correspondente a cada ponto visto no espectro mostrado. Quanto maior o número de vezes a se varrer uma dada região, maior o número de pontos a participar da média, e menor a dispersão dos pontos médios experimentais ao redor dos valores ideais que seriam obtidos para um número de varreduras “infinito ”.

A dispersão dos valores médios experimentais ao redor dos respectivos valores médios ideais, mais especificamente falando, o desvio relativo dos valores em torno da média idealizada, decresce, para incertezas aleatórias como as consideradas, com a raiz quadrada do número de pontos a participar da média.^[3] Assim, quanto maior o número de varreduras considerado, mais “lisa” será a curva final obtida no espectro. Em troca, um maior tempo de medida será demandado e, portanto, uma relação de custo benefício deve ser, ai, considerada. Curvas precisas exigem um considerável número de varreduras que podem vir a tomar horas de trabalho.

Obtendo Informações dos Espectros

XPS: análise do pico Ga3d. A análise consiste na remoção dos elétrons secundários - neste caso mediante a remoção por base linear - seguindo do ajuste de uma função analítica sobre os pontos experimentais - no caso uma função gaussiana. Os dados obtidos dos ajustes fornecem as informações físicas procuradas.

Espectros XPS são caracterizados por uma coletânea de pontos que apresentam flutuações características, o que implica, como já citado, em uma dispersão dos pontos experimentais ao redor dos valores ideais. A extração de informações dos espectros XPS exige em uma segunda etapa, mediante o uso de programa de processamento adequado a tal fim,^[4] o tratamento e o ajuste estatístico de uma função analítica sobre os dados de cada um dos picos de interesse do espectro, dos quais resultam informações confiáveis e relevantes sobre os valores das áreas, posições e larguras dos picos de interesse. A partir destes resultados é que informações física relevantes serão inferidas.

O primeiro procedimento na análise de um pico consiste na remoção dos “elétrons de fundo”, da base na qual este se assenta. O processo mais simples para a remoção dos elétrons de fundo consiste na extração de uma base linear sob o pico no espectro original, sendo aplicável sempre que a correta identificação das posições de pontos base do pico é possível. Na maioria dos casos que envolvem semicondutores, este é o caso.

O ajuste de uma função analítica pode ser feito empiricamente ou procurando-se razões experimentais e teóricas para escolher-se a função para o ajuste, e neste caso geralmente funções gaussianas, lorentzianas, ou em certos casos uma convolução das duas prestam-se bem ao serviço de ajuste aos dados experimentais. Em sua quase totalidade os ajustes destas funções a um mesmo pico fornecem resultados semelhantes para área, posição e largura de cada pico considerado, diferindo os resultados entre os ajustes por valores menores do que as incertezas nos resultados obtidos. Na figura vemos o ajuste do pico Ga3d para um espectro obtido de uma amostra de arseneto de gálio onde depositou-se uma pequena quantidade de césio na superfície. O ajuste é feito mediante uma função gaussiana, e o ajuste por lorentziana fornece resultados bem semelhantes.

$${\displaystyle A=A_{0}+{\frac {A_{1}}{w{\sqrt {\frac {\pi }{2}}}}}e^{-2({\frac {(x-x_{c})}{w}})^{2}}}$$

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

uma função gaussiana típica usada na análise de espectros XPS: os parâmetros A₀, A₁, X_c e W são ajustados pelo programa de análise de forma que a curva ajuste-se da melhor forma possível aos dados experimentais.

Em metais a remoção de uma base linear pode não mostrar-se adequada devido a uma considerável elevação do patamar de elétrons secundários no lado do pico correspondente a menores energias cinéticas, sendo exemplo deste caso o pico Fe3p em espectros de Ferro (figura abaixo, espectro para 150A de Fe). Basicamente as estruturas são simétricas para materiais isolantes e semicondutores, mas não para metais, e um tratamento diferenciado para a remoção dos elétrons secundários faz-se então necessário. Nesse último caso uma função do tipo Doniach-Sunijic ou uma aproximação desta presta-se bem melhor à correta remoção da base formada pelos elétrons secundários e o uso de uma base linear é desencorajado.

Modelo de Drude (em azul)

O modelo Drude de condução elétrica foi proposto em 1900 ^[1][2] por Paul Drude para explicar as propriedades de transporte de elétrons em materiais (especialmente metais). Basicamente, a lei de Ohm estava bem estabelecida e afirmava que a corrente J e a tensão V que impulsionam a corrente estão relacionadas à resistência R do material. O inverso da resistência é conhecido como condutância. Quando consideramos um metal de comprimento unitário e área de seção transversal, a condutância é conhecida como condutividade, que é o inverso da resistividade. O modelo de Drude tenta explicar a resistividade de um condutor em termos do espalhamento de elétrons (os portadores de eletricidade) pelos íons relativamente imóveis no metal que agem como obstruções ao fluxo de elétrons.

O modelo, que é uma aplicação da teoria cinética, assume que o comportamento microscópico dos elétrons em um sólido pode ser tratado classicamente e se comporta de maneira muito semelhante a uma máquina de pinball, com um mar de elétrons em constante agitação, saltando e voltando a saltar mais pesados, íons positivos relativamente imóveis.

Os dois resultados mais significativos do modelo Drude são uma equação eletrônica de movimento,

${\displaystyle {\frac {d}{dt}}\langle \mathbf {p} (t)\rangle =q\left(\mathbf {E} +{\frac {\langle \mathbf {p} (t)\rangle \times \mathbf {B} }{m}}\right)-{\frac {\langle \mathbf {p} (t)\rangle }{\tau }},}$

e uma relação linear entre a densidade de corrente J e o campo elétrico E,

${\displaystyle \mathbf {J} =\left({\frac {nq^{2}\tau }{m}}\right)\mathbf {E} .}$

Aqui o tempo é descrito por ${\displaystyle t}$, ${\displaystyle \langle p\rangle }$ é o momento médio por elétron e ${\displaystyle q}$, ${\displaystyle n}$, ${\displaystyle m}$ e ${\displaystyle \tau }$ são, respectivamente, a carga do elétron, densidade numérica, massa e tempo livre médio entre as colisões iônicas. A última expressão é particularmente importante porque explica em termos semi quantitativos por que a lei de Ohm, uma das relações mais onipresentes em todo o eletromagnetismo, deve ser válida.^[3][4]

O modelo foi estendido em 1905 por Hendrik Antoon Lorentz (e, portanto, também é conhecido como o modelo Drude-Lorentz) Para dar a relação entre a condutividade térmica e a condutividade elétrica dos metais, e é um modelo clássico. Mais tarde, foi complementado com os resultados da teoria quântica em 1933 por Arnold Sommerfeld e Hans Bethe, levando ao modelo Drude-Sommerfeld.

Índice

• 1Histórico
• 2Explicação
• 3Problemas do modelo
• 4Ver também
• 5Referências

Histórico

O físico alemão Paul Drude propôs seu modelo em 1900, quando a existência de átomos não estava clara, e não estava claro que os átomos estavam em uma escala microscópica.^[5] A primeira prova direta da existência de átomos através do cômputo do número de Avogadro num modelo microscópico é devida a Albert Einstein. O primeiro modelo moderno da estrutura atômica, devido a J.J. Thomson, data de 1904, e o posterior modelo de Rutherford, data de 1909. Drude iniciou seu trabalho a partir da descoberta dos elétrons, em 1897, por J.J. Thomson, assumindo como um modelo de sólidos simplificado, onde a região sólida é composta de centros de espalhamento positivamente carregados, e um mar de elétrons submersos no entorno destes centros de espalhamento, fazendo com que o sólido seja totalmente neutro eletricamente.^[6]

Explicação

O modelo de Drude supõe que um portador médio de carga elétrica está sujeito à ação de uma `força de resistência' ${\displaystyle \,\gamma }$. Em presença de um campo elétrico externo E satisfaz-se a seguinte equação diferencial:

${\displaystyle m{\frac {d}{dt}}\langle {\vec {v}}\rangle =q{\vec {E}}-\gamma \langle {\vec {v}}\rangle }$

onde ${\displaystyle \langle {\vec {v}}\rangle }$ é a velocidade média, m é a massa efectiva e q a carga elétrica do portador de carga.

A solução estacionária (${\displaystyle {\frac {d}{dt}}\langle {\vec {v}}\rangle =0}$) desta equação diferencial é:

${\displaystyle \langle {\vec {v}}\rangle ={\frac {q\tau }{m}}{\vec {E}}=\mu {\vec {E}}}$

onde:

${\displaystyle \,\tau ={\frac {m}{\gamma }}}$ é o tempo livre médio de um portador de carga, e ${\displaystyle \,\mu }$ é a mobilidade elétrica. Se se introduz a densidade do gás de portadores de carga n (partículas por unidade de volume), podemos relacionar a velocidade média com uma corrente elétrica:

${\displaystyle {\vec {J}}=nq\langle {\vec {v}}\rangle }$

Pode-se demonstrar que o material satisfaz a lei de Ohm com uma condutividade elétrica em corrente contínua ${\displaystyle \,\sigma _{0}}$.

${\displaystyle {\vec {J}}={\frac {nq^{2}\tau }{m}}{\vec {E}}=\sigma _{0}{\vec {E}}}$

O modelo de Drude permite também predizer a corrente como uma resposta a um campo elétrico variável no tempo com uma frequência angular ${\displaystyle \,\omega }$, em cujo caso:

${\displaystyle \sigma (\omega )={\frac {\sigma _{0}}{1+i\omega \tau }}}$

Onde se supõe que:

${\displaystyle E(t)=\Re (E_{0}e^{i\omega t})}$

${\displaystyle J(t)=\Re (\sigma (\omega )E_{0}e^{i\omega t})}$

Em outras convenções, \, i é substituido por \, -i em todas as equações. A parte imaginária indica que a corrente está atrasada com respeito ao campo elétrico, o que se produz porque os elétrons necessitam aproximadamente um tempo ${\displaystyle \,\tau }$ para acelerarem-se em resposta a uma mudança eo campo elétrico aplicado. No caso prévio o modelo de Drude aplicou-se aos elétrons, mas também pode ser aplicado a buracos, quer dizer, aos portadores de carga positiva nos semicondutores.

Problemas do modelo

Este modelo simples oferece uma boa explicação para a condutividade de corrente contínua e corrente alterna em metais, o efeito Hall, e a condutividade térmica (devida a elétrons) em metais, mas falha ao não providenciar uma explicação para a disparidade entre as capacidades caloríficas dos metais em comparação com a dos materiais isolantes. Num isolante elétrico, esperar-se-ia que a capacidade térmica fosse zero, dado que não existem elétrons livres. Na realidade, os metais e os isolantes elétricos possuem aproximadamente a mesma capacidade térmica à temperatura ambiente. O modelo de Drude também falha em explicar a existência de portadores de carga aparentemente positivos como demonstra o efeito Hall.

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Energia de bandgap

A largura da banda proibida se torna maior no regime de confinamento forte, uma vez que os níveis de energia se dividem acima. O raio de Bohr do éxciton pode ser expresso como:

${\displaystyle a_{b}^{*}=\varepsilon _{2}\left({\frac {m}{\mu }}\right)a_{b}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde a_b é o raio de Bohr = 0.053 nm, m é a massa, ${\displaystyle \mu }$ é a massa reduzida e ${\displaystyle \varepsilon _{r}}$ é a constante dielétrica dependente do tamanho (permissividade relativa). Isto resulta num aumento na energia total de emissão (a soma dos níveis de energia nos bandgaps menores no regime de confinamento forte é maior que os níveis de energia no bandgap dos níveis originais no regime de confinamento fraco) e a emissão a vários comprimentos de onda. Se a distribuição de tamanhos dos pontos quânticos não é estreita o suficiente, a convolução de múltiplos comprimentos de onda de emissão é observado como um espectro contínuo.^{[carece de fontes]}

Energia de confinamento

A entidade éxciton pode ser modelada usando a partícula na caixa. O elétron e a lacuna podem ser vistos como o hidrogênio no modelo de Bohr, com o núcleo do hidrogênio sendo substituídos pela lacuna de carga positiva e massa do elétron negativa. Então os níveis de energia do éxciton podem ser representados como a solução para a partícula na caixa no nível fundamental (n = 1), com a massa sendo substituída pela massa reduzida. Variando o tamanho do ponto quântico, a energia de confinamento do éxciton pode ser controlada.^{[carece de fontes]}

Energia de ligação do éxciton

Há uma energia de atração eletrostática entre o elétron carregado negativamente e a lacuna carregada positivamente. A energia envolvida na atração é proporcional à energia de Rydberg e inversamente proporcional ao quadrado da constante dielétrica dependente do tamanho do semicondutor.^[70] Quando o tamanho do cristal semicondutor é menor que o raio de Bohr do éxciton, a interação Coulômbica precisa ser modificada para se adaptar à situação.

Portanto, a soma destas energias pode ser representada como:

${\displaystyle E_{confinamento}={\frac {\hbar ^{2}\pi ^{2}}{2a^{2}}}\left({\frac {1}{m_{e}}}+{\frac {1}{m_{h}}}\right)={\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E_{exciton}=-{\frac {1}{\epsilon _{2}^{3}}}{\frac {\mu }{m_{e}}}R_{y}=-R_{y}^{*}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E=E_{bandgap}+E_{confinamento}+E_{exciton}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E=E_{bandgap}+{\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}-R_{y}^{*}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde ${\displaystyle \mu }$ é a massa reduzida, a é o raio, m_e é a massa do elétron livre, m_h é a massa da lacuna e ε_r é a constante dielétrica dependente do tamanho.

Apesar das equações acima terem sido derivadas usando premissas simplificadas, elas implicam que as transições eletrônicas dos pontos quânticos dependerão do seu tamanho. Estes efeitos de confinamento quântico são aparentes somente abaixo do tamanho crítico. Partículas grandes não exibem este efeito. Este efeito de confinamento quântico em pontos quânticos tem sido verificado experimentalmente repetidas vezes e é uma característica chave de muitas estruturas eletrônicas emergentes.^[71]

A interação eletrostática entre os portadores de carga confinados também pode ser estudada por meios numéricos quando resultados não restritos em aproximações assintóticas são buscados.^[72]

Modelos

Uma variedade de estruturas teóricas existem para modelar propriedades ópticas, eletrônicas e estruturais dos pontos quânticos. Estas podem ser amplamente divididas em mecânica quântica, semiclássica e clássica.^{[carece de fontes]}

Mecânica quântica

Modelos e simulações de pontos quânticos baseados em mecânica quântica frequentemente envolvem a interação dos elétrons com uma matriz randômica ou pseudopotencial.^[73]

Semiclássica

Modelos semiclássicos de pontos quânticos frequentemente incorporam um potencial químico. Por exemplo, o potencial químico termodinâmico de um sistema de N partículas é dado por:

${\displaystyle \mu {\bigl (}N{\bigr )}=E{\bigl (}N{\bigr )}-E{\bigl (}N-1{\bigr )}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Cujos termos de energia podem ser obtidos como soluções da Equação de Schrödinger. A definição de capacitância:

${\displaystyle {\frac {1}{C}}\equiv {\frac {\Delta V}{\Delta Q}}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Com a diferença de potencial:

${\displaystyle \Delta V={\frac {\Delta \mu }{e}}={\frac {\mu (N+\Delta N)-\mu (N)}{e}}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Pode ser aplicada para um ponto quântico com a adição ou remoção de elétrons individuais, ${\displaystyle \Delta N=1}$e ${\displaystyle \Delta Q=e}$.

Então:

${\displaystyle C(N)={\frac {e^{2}}{\mu (N+1)-\mu (N)}}={\frac {e^{2}}{I(N)-A(N)}}}$///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

É a capacitância quântica de um ponto quântico, onde I(N) foi denotado como o potencial de ionização e A(N) a afinidade eletrônica do sistema de N partículas.^[74]

///////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Sistemas dialético-pujantes

Em assunto, Definição

Sistemas dialético-pujantes^[1] são molas com a capacidade ou característica de variar reversivelmente sua constante elástica para atender demandas de cargas afins, o que é feito por meio de modulação mecânica ou eletromecânica, estes sistemas foram criados no Instituto Federal do Maranhão na cidade Zé Doca, no ano de 2013, pelos pesquisadores Welton Martins (autor e então graduando em química), Wild Lago (Professor e pesquisador da disciplina Física), com incentivo e correções de Davina Chaves (Professora e pesquisadora). Sendo ainda estudados e reproduzidos com finalidade de melhoramento para aplicação na industria automobilística e de bens em geral, estes sistemas tem grande potencial de aplicação e representaram a "quebra" do princípio da invariabilidade^[2] da constante elástica de corpos a uma mesma temperatura. Ou seja segundo a teoria de sistemas dialético-pujantes, um mesmo corpo^[3], a uma mesma temperatura pode apresentar muitas constantes elásticas, as quais podem ser manipuladas mecanicamente, sem necessidade do emprego de energia térmica, tal como se faz atualmente para modificar as propriedades elásticas de alguns materiais, assim as constantes elásticas podem mudar em sistemas dialético-pujantes^[1].

Definição matemática para estes sistemas

A descrição matemática de sistemas dialético-pujantes é definida com base na deformação do corpo interno e sua resposta no comportamento elástico do sistema. Designando-se como sendo artificiais os sistemas que são sintéticos. Pode-se utilizar como equação descritiva a seguinte:

• 

  Equação 1///////////
  

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

As deformações dos sistemas dialético-pujantes podem ser calculadas por meio da equação a cima, onde x_2 é a nova deformação do sistema mediante modulação, tci é a tensão do corpo interno, tp% é o percentual da tensão que foi perdido kci é a constante elástica do corpo interno, ds é a deformação anterior do sistema, dci é deformação anterior do corpo interno e x1 é a deformação anterior do sistema. Os sistemas dialético-pujantes são multifuncionais e as tecnologias para eles ainda são bastante novas quanto a seus componentes intrínsecos e sua aceitação. Todavia a utilização desta tecnologia em veículos resulta na possibilidade de fornecer ao mesmo, máxima capacidade de carga, sem sofrer deformação e com mesma capacidade de amortecimento (MARTINS, 2016). Assim, para verificar a nova constante elástica gerada basta acrescentar o valor de x_2 em F=K.x, substituindo-se x por x_2, logo um sistema dialético-pujante pode ser conforme figura 2, um sistema onde para cada constante elástica existe um novo comportamento mecânico^[1]:

• 

  Figura 1

^[1] O resultado da equação apresentada, mostrado na figura a cima é um gráfico, tal como gráfico 1, capaz de relacionar a nova constante elástica gerada e a deformação do sistema. logo a relação entre as constantes pode ser descrita como^[1]:

• 

  Gráfico 1

^[1]

Como são e como surgiram

Esta categoria de sistema foi criada, inicialmente a partir de um “in site” seguido de observações experimentos com uma liga de dinheiro (elastômero) e um canudinho (plástico), submetido a aproximadamente 200 ensaios mecânicos^[2] de flexão longitudinal e transversal. Posteriormente, os conceitos foram levados em nível de estudo teóricos de corpos elásticos, levantamento de hipótese e rigorosos testes experimentais com material de engenharia, deduções matemáticas e tentativas e erros. É ilustrado na figura 2 os tipos mais comuns de sistemas dialético-pujantes.

• 

  Formas básicas de sistemas dialético-pujantes

Existem pelo meno 10 equações que se relacionam ao comportamento elástico de cada corpo, entretanto, ainda são limitadas e necessitam de mais estudos com intuito de melhorar suas descrições matemáticas.

A pesquisa surgiu quando o pesquisador segurava um canudo e uma liga elástica de amarrar dinheiro e lia uma notícia sobre a modalidade exportiva "salto com vara", onde mostrava-se que a vara da atleta Fabiana Murer havia se quebrado em um salto devido a problemas de resistência elástica, então para sanar o problema de cada vara ser produzida para um atleta específico, iniciou-se a criação de um dispositivo que pudesse ser utilizado por variais pessoas, capaz de quebrar o princípio da invariabilidade da constante elástica.

Tecnologias básicas de sistemas dialético pujantes

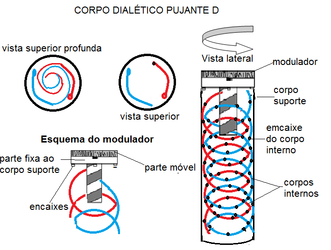
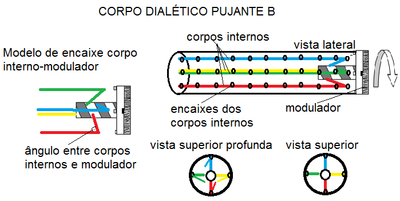
Sistemas dialético-pujantes tem sua tecnologia ainda em desenvolvimento, mas podem ser aplicadas de bicicleta até pontes resistentes e preparadas para se adaptar a demanda elástica solicitada em um dado evento. A tecnologia de modulação pode ser mecânica ou eletrônica, podendo ter sistemas integrados ou apenas engrenagens. O conceito base para compreensão de sistemas dialético-pujantes é a ideia de uma barra oca com um fio elástico em seu interior, o que na medida em que o fio elástico é tencionado e preso na barra, passa a formar um sistema que a cada alteração de tensão no corpo provoca modificações no sistema como um todo. É uma forma mecânica de gerenciar a energia que pode deformar um corpo e quanto essa energia pode deformá-lo.^[1]

São muitas as equações que os descrevem e suas aplicações e formas de fabricação, um exemplo típico e bastante simples pode ser mostrado conforme figura 3 e 4.

• 

  Figura 3

 
• 

  Figura 4

Em ambas as figuras a cima a modulação é realizada girando-se o modulador para aumentar ou diminuir a tensão dos corpos internos, o que modifica as propriedades de resistência do sistema a demandas de cargas externas.

A primeira literatura que trata dessa tecnologia, aberta ao publico atualmente é o livro Princípios de elasticidade e teoria da constante variável^[1] lançado em 2016, o que justifica a pouca disponibilidade de conteúdo sobre o tema.